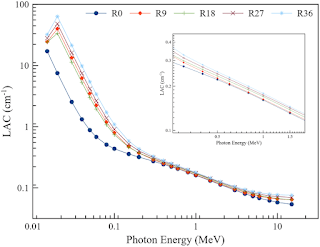
LINEAR ATTENUATION COEFFICIENT

Linear attenuation coefficient (LAC)

Linear attenuation coefficient

The linear attenuation coefficient (LAC) is a measure of the ability of a material to absorb X-rays or other forms of electromagnetic radiation. It is defined as the fraction of photons absorbed per unit thickness of the material. The unit of linear attenuation coefficient is typically cm-1. The linear attenuation coefficient of a material is determined by several factors, including the atomic number and electron density of the atoms in the material, as well as the energy of the X-rays. Higher atomic number and electron density tend to result in higher linear attenuation coefficients.

Additionally, the linear attenuation coefficient also increases with the energy of the X-rays. The linear attenuation coefficient is an important parameter in X-ray imaging, particularly in computed tomography (CT) imaging, where it is used to reconstruct images of the internal structure of an object. The linear attenuation coefficient of different materials can be measured and used to calculate the absorbed dose of radiation. linear attenuation coefficient can also be used to calculate the transmission of X-rays through a material, which is useful in industrial imaging applications such as non-destructive testing. In medical imaging, the linear attenuation coefficient is used to determine the amount of radiation that is absorbed by different tissues in the body, which is important for determining the radiation dose received by patients. linear attenuation coefficient is also used to determine the contrast between different tissues in medical images, which can be used to improve the diagnostic accuracy of imaging studies. 

CALCULATING µ 

The intensity of the beam at distance x (cm) within a material is calculated using the following equation: 

Ix=I0.e−μx 

Where Ix is the intensity at depth of x cm, 

I0 is the initial intensity, and 

µ is the linear attenuation coefficient. 

Rearrange and take the log of both sides giving the equation for µ. 

μ = ln(Io/Ix)/x